- Pitch
- Loudness
- Timbre
A physicist would describe the same tone in terms of three quantities:
- Frequency
- Intensity
- Overtone or Harmonic Structure
Loudness = Intensity (+ substantial frequency and overtone corrections)
Timbre = Overtone Structure (+ frequency, intensity corrections)
The first observation is that musical tones are generally (almost) periodic . This is an important concept so we should illustrate it.
Listen to the following mp3 file of four sounds. The sounds, in the order I made them, were
- a finger being rubbed around the rim of a wine glass
- a wooden whistle
- the little siren I demonstrated in the second lecture
- the human (my) voice, singing "aah"
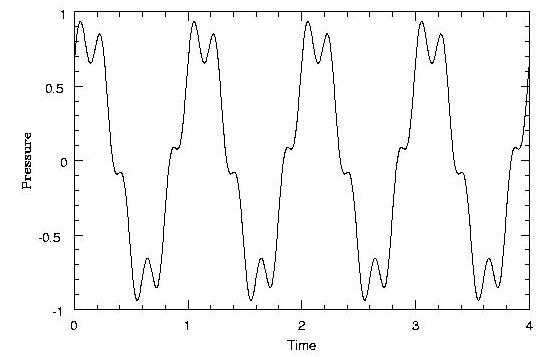
Each of these sounds was sampled with a microphone. The pressure, as a function of time, looked like this:
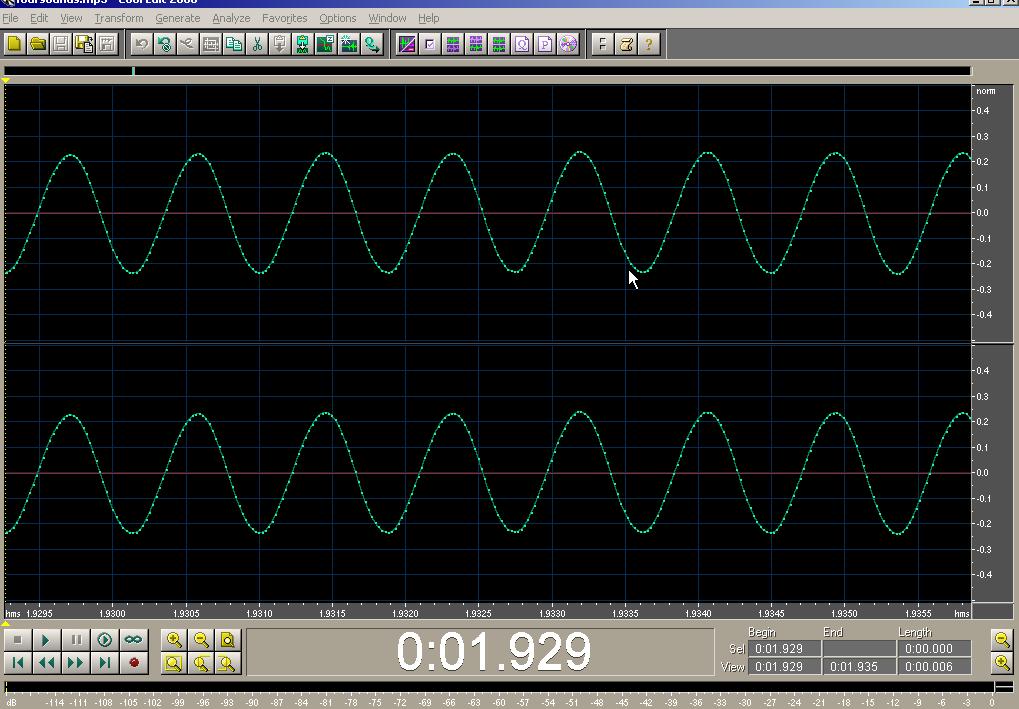
Above: the wine glass. Below: the whistle
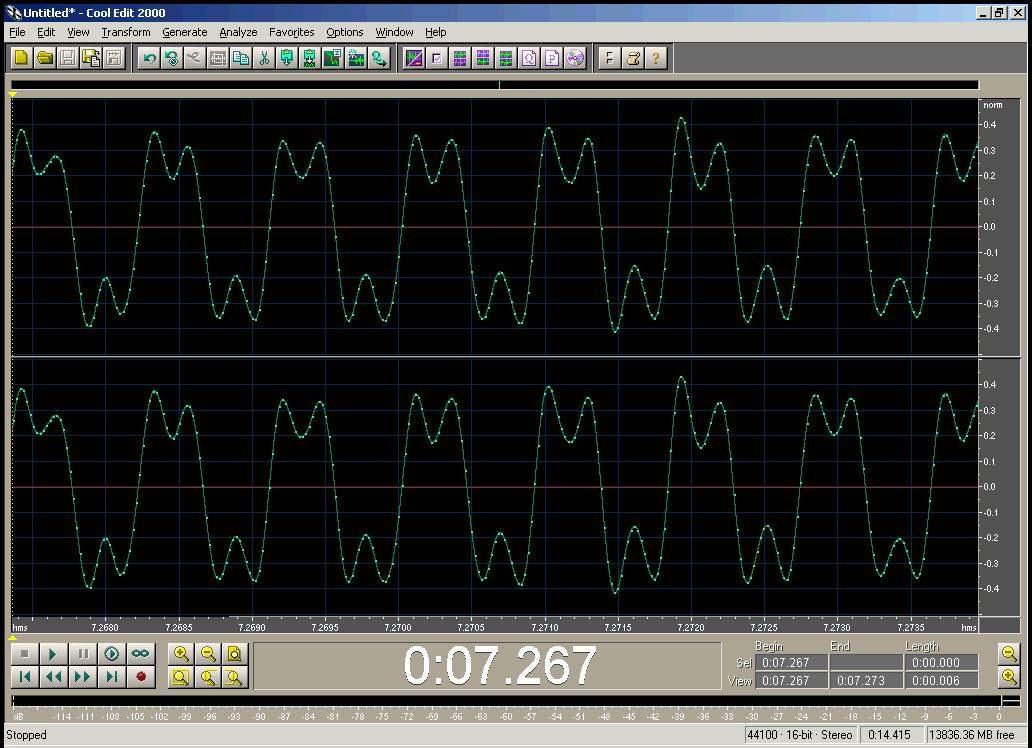
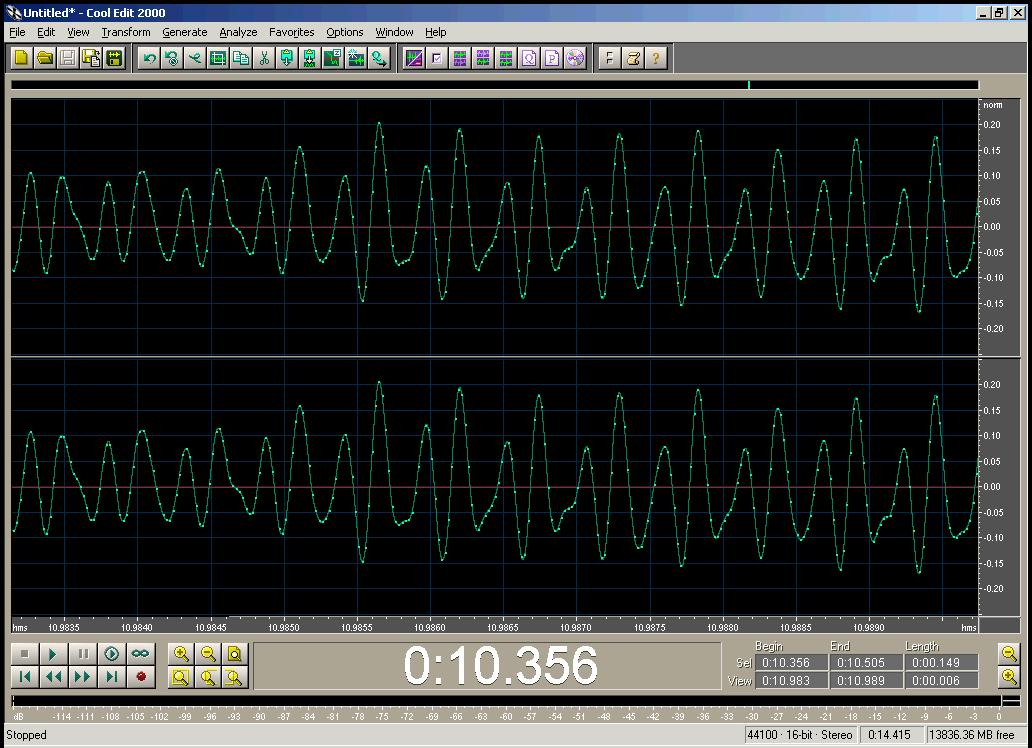
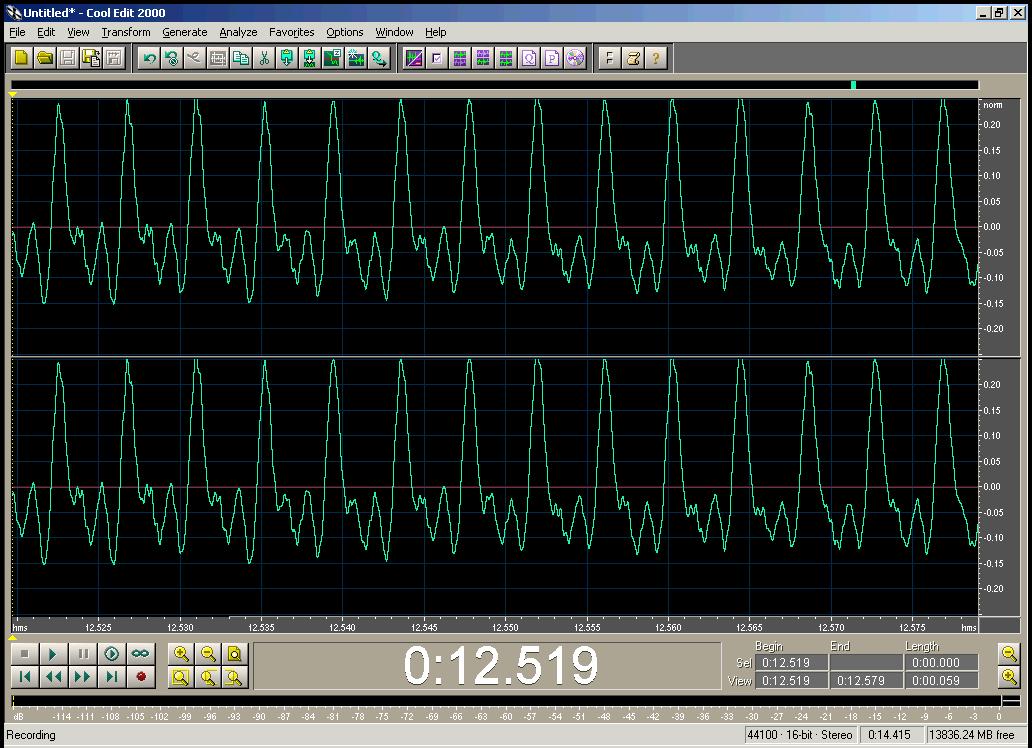
Above, the siren. Below, the voice.
These recordings were made using software called Syntrillium Cool Edit;
Syntrillium has been bought out by Adobe, which renamed it Adobe
Audition. You can learn about it
here .
The thing to notice about all four pictures is that the pressure pattern
repeats over and over. In physics we call something which repeats like
this periodic . The fact that these sounds are periodic, is the
key to their having definite pitches. In fact, we can even say,
Sounds which are periodic have a definite pitch. Sounds with a definite pitch are periodic.
Of course nothing is perfectly periodic. However, musical sounds come surprisingly close.Obviously we need language to describe periodic functions. The most basic property is the period , which is just the time that it takes for the pattern to repeat. This is the same as the time difference between when some pattern appears, and when it appears again. For instance, in this plot,
the period is 1 because every 1 on the horizontal axis, the pattern repeats.
Frequency is defined as the inverse of the period. Period is usually written as T, and is measured in seconds. Frequency is f = 1/T and is measured in 1/seconds, which are called Hertz. Think of Hertz as "somethings per second," specifically, how often something repeats per second. The more often something repeats, the shorter the period, but the larger the frequency.
The most familiar example to musicians is metronomic markings. At a "moderato" tempo of 100 beats per minute, the period is (60 seconds/100 beats) = 0.6 seconds. The frequency is 1/period = 1/(0.6 seconds) = 1.67 Hertz. Since there are 2 eighth notes in a quarter note, the frequency of 8'th notes is twice as high; sixteenth notes are twice as high again, so sixteenth notes in moderato tempo occur at a frequency of about 4/(0.6 seconds) = 6.67 Hertz.
If something makes a series of sharp sounds, like staccato notes or like something bouncing in bicycle spokes, your ear can distinguish them as separate sounds if they are spaced less than about 12 or 15 per second. Beyond that, your perception tends to blur them together. [This is why musicians can get away with replacing a series of very fast notes with a slur sometimes without anyone noticing.] At about 20 to 30 Hertz, you instead perceive them as forming a low, dull sound. As the frequency goes up, the interpretation as a sound of definite frequency becomes clearer.
You can test this by putting a bicycle in a high gear, flipping it
upside down so you can spin the back wheel with the pedal, and sticking
a pen or piece of cardboard into the spokes. Depending on the speed you
spin the wheel, you can make the object strike the spokes anywhere from
a few times to a few hundred times per second. When it goes above 40 or
50 times a second, it is easily recognizable as a pitch. The faster you
spin the wheel, the higher the pitch, eaching us that
Pitch corresponds to the frequency of a sound. Higher frequency is higher pitch.
There are many ways to convince yourself of that.
The limits of the range of Human hearing are about 20 Hertz to about 17 000 Hertz. At the bottom end, your ear's sensitivity becomes very poor, and sound becomes more of a sensation than a hearing experience. It is hard to demonstrate because most things which make a low pitched sound are also making higher pitched sounds at the same time [overtones, the subject of future lectures], and what you hear is the higher pitched tones. For instance, for the deepest instruments, like the contrabassoon, the bottom range of the piano, or the E string on the string bass, your perception is based almost entirely on these higher frequencies [overtones] rather than the fundamental note itself.
That is not true of the top range of hearing. Again, you lose sensitivity above some frequency, but in a sharper way. Sounds outside your range of hearing are simply not perceived at all. To see this, listen (on headphones or speakers) to the following mp3 file, which plays in succession, notes of
- 11 000 Hertz
- 12 000 Hertz
- 13 000 Hertz
- 14 000 Hertz
- 15 000 Hertz
- 16 000 Hertz
- 17 000 Hertz
- 18 000 Hertz
- 19 000 Hertz
- 20 000 Hertz
Higher frequency is higher pitch, but we also have a definite notion of how much higher pitched one note is than another. Is this determined in a simple way in terms of the periods or frequencies? The answer is yes, but not as simple as you were hoping.
this mp3 file plays, in succession, notes of frequency
- 500 Hertz
- 1 500 Hertz
- 2 500 Hertz
- 3 500 Hertz
- 4 500 Hertz
- 5 500 Hertz
- 6 500 Hertz
Is it even spacings in period? this mp3 file plays, in succession, notes of
- period 1/2000 sec, or frequency 2000 Hertz
- period 3/2000 sec, or frequency 667 Hertz
- period 5/2000 sec, or frequency 400 Hertz
- period 7/2000 sec, or frequency 285.7 Hertz
- period 9/2000 sec, or frequency 222 Hertz
- period 11/2000 sec, or frequency 181.2 Hertz
- period 13/2000 sec, or frequency 153.8 Hertz
Let us try equal ratios of frequency, say, each note exactly twice the frequency of the note before. this mp3 file plays notes of frequency
- 220 Hertz
- 440 Hertz
- 880 Hertz
- 1760 Hertz
- 3520 Hertz
- 7040 Hertz
To confirm this, we play notes spaced by factors of 3/2: this mp3 file plays notes spaced by this ratio, namely,
- 440 Hertz
- 660 Hertz
- 990 Hertz
- 1485 Hertz
- 2227 Hertz
- 3341 Hertz
- 5012 Hertz
This tells us that our perception of pitch is logarithmically related to frequency, and since the octave is the most important musical interval, we should study this using logarithms base 2. (More in the next lecture)