The answer to "why" must be evolutionary. We encounter a wide range of frequencies in our lives. There is important sound information throughout that frequency range. Telling apart a 150 Hertz tone from a 200 Hertz tone can tell you if someone is nervous or scared. Much of the information in speech is in the 3000 Hertz range. We need good sensitivity and need to make perceptual distinctions through this range.
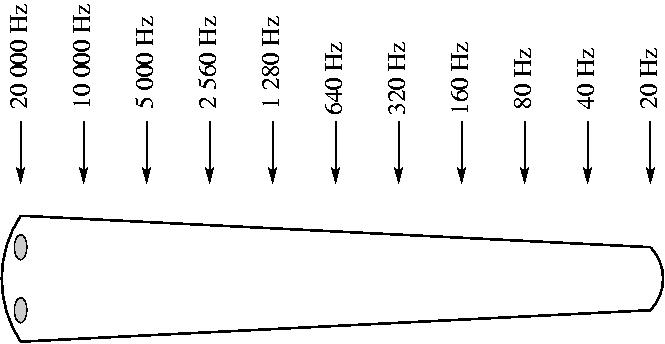
The answer to "how" lies in the cochlea. Sine wave pressure variations excite different spots in the cochlea depending on the frequency of the sine wave. (Sine waves are one special periodic function, which turn out to play a special role. We will talk about why and how in future lectures.) The unwound cochlea is about 34 millimeters long. Every factor of 2 in frequency moves the spot that gets vibrated by 3.4 millimeters along the cochlea. Thus, our sense of frequency difference corresponds to how far along the cochlea a sound appears. In cartoon form, think of it like this:

The highest frequencies cause fluctuations at the beginning of the cochlea near the oval and round windows, the lowest frequencies cause fluctuations near the end.
[The musicians might visualize it better this way:

showing that the location on the cochlea depends on the note, and that almost half the range of hearing lies above the top of treble clef, and a fair bit lies below bass clef.]
A sound of a definite frequency does not actually vibrate the membranes in the cochlea at one point. Rather, there is one point where the vibration is biggest, and a range around that value where the vibration is big enough to be important. This range on the cochlea is called the critical band excited by a sound. It covers frequencies about 10% to 15% higher and lower than the note which is played. The flexing of the cochlea falls away as you move from the center of the band. The picture to have in your mind is something like this:
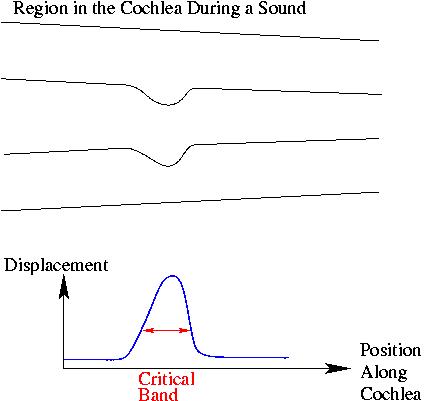
Note that the critical band does not have clear edges. There is a little vibration some distance away on the cochlea, even where the nominal frequency is almost a factor of 2 different. The spread is higher on the high frequency side than on the low frequency side.
The size of this region turns out to be smaller in living than in dead cochleas. (Don't ask how they did the measurements.) This has to do with the outer hair cells. Apparently, they respond to stimulus, not by sending a nerve signal, but by flexing or moving their stereocilia in a way which changes the tension and motion of the cochlear membranes. This enhances the motion at the center of the critical band and narrows the size of the band.
Although a region covering about a 10% change in frequency makes a nervous response, you are able to distinguish a much smaller change in frequency than this. That is because your brain can determine the center of the excited region much more accurately than the width of that region.
The size of a change in frequency which you can just barely distinguish as different, is called the Just Noticable Difference (because you can just barely notice the difference). Listen to this mp3 file to see how sensitive your ear is to a small change in frequency. It plays ten tones. Each one starts out at 600 Hertz, but shifts. For the first two, this shift is by 4%, that is, by 24 Hertz; in one it shifts up, in one it shifts down. The next pair, the shift is 2%, or 12 Hertz; then 1% or 6 Hertz, then 0.5% or 3 Hertz, then 0.25% or 1.5 Hertz.
The challenge is to tell which of each pair has the "up" shift and which has the "down" shift. For the 4% and 2% changes, you will find it very easy. For the 1% it is not hard. For the 0.5% you can probably just barely tell, and for the 0.25% you probably cannot tell. Therefore, your JND at 600 Hertz is around 0.5%.
The JND (Just Noticable Difference) is frequency dependent. Your ear is less accurate at low frequencies, especially below about 200 Hertz. It is also somewhat individual dependent. However, the percent change you can sense is about the same 0.5% across most of the range of hearing.
People who know and understand logarithms should skip the rest of this lecture.
Since a factor of 2 in frequency has a deep musical meaning (in fact, if two notes differ by a factor of 2 musicians write them using the same letter), it makes the most sense to use logarithms base 2 to describe frequencies.
I will write log base two of a number x as Log_2(x). What Log_2(x) means is, "how many 2's must I multiply to get the number x?" For instance,
You can also take logs of numbers which are not some power of 2. In fact, insisting that Log_2(x*y) = Log_2(x) + Log_2(y) is enough to tell uniquely what Log_2(x) should be for any (positive) x. Fractional powers follow the rule I showed.
For instance, Log_2( square root of 2 ) is 1/2, that is, Log_2(1.414) = 0.5.
You can also define Log_10(x) as the number of factors of 10 it takes to get x, so Log_10(1000) = 3 because 1000 = 10 * 10 * 10, which took 3 10's. We will use this more when we do intensitites.
If your calculator will only do Log_10 and not Log_2, you should know that
Log_10(2) = 0.3
Log_2(10) = 3 1/3 = 3.33
These are "good enough for homeworks".