These statements are true so long as
What linearity means is that a complex sound--say, an orchestra--can be described as the sum of simple sounds--say, each instrument. Sometimes, your ear can make the separation between these sounds (though not always, as we discuss when we talk about masking).
We have already seen that musical sounds, at least the ones of definite pitch, are periodic. But they are not generally sinusoidal. This matters because everything we said last lecture, about how a sound causes vibration on the cochlea, is true of sine wave sounds. The purpose of this lecture is to start seeing why that understanding is still good enough to describe complicated sounds, and what goes on when a complicated sound enters your ear.
This MP3 file plays a sine wave, triangle wave, square wave, and sawtooth wave, as well as a voice "singing" (quotes, because it was me) "ooo" and "eee". The wave forms of "ooo" and "eee" are shown at the end of this page. The computer generated waves have the same frequency, 440 Hertz, and the sung notes have the same frequency, 256 Hertz. They sound very different, that is, they have different timbre.
Can we describe timbre more precisely? Yes. That is because of a powerful piece of mathematics, called Fourier analysis, which says that any periodic function--say, the pressure pattern from an instrument--can be viewed as the sum of many sine waves.
We saw last time that a sine wave which repeats with frequency f is generally of form,

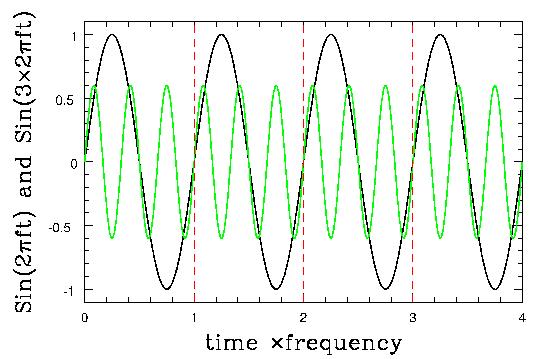
which shows four periods of a wave with a certain frequency, and a wave with exactly 3 times the frequency. Both waves certainly repeat at each point where the red line is drawn.
If we add together one sine wave which repeats with period T, and another which repeats twice or three times as often, the resulting sum will repeat with period T. It will not repeat with period T/2 or T/3, since one of the waves which built it does not. However, all of them repeat with period T, so the sum will too.
To understand how to add together two waves, look at this illustration:
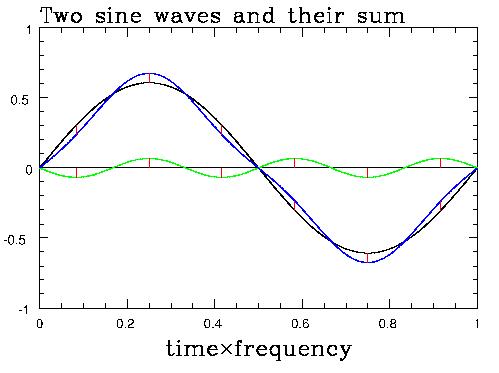
which illustrates the summation of two waves, one with 3 times the period of the other. You see how much the smaller wave moves up and down with respect to the axis, and you move up and down the same amount with respect to the larger wave.
Now for Fourier analysis:
First, let me explain the claim. Suppose you have the pressure pattern for an instrument or something, which is periodic with period T=1/f. The claim is that there are coefficients P_1, P_2, P_3, etc, and phases phi_1, phi_2, phi_3 etc, such that
P - P(atmospheric) = P_1 sin( 1 * 2 pi ft + phi_1) + P_2 sin( 2 * 2 pi ft + phi_2) + P_3 sin( 3 * 2 pi ft + phi_3) + P_4 sin( 4 * 2 pi ft + phi_4) + P_5 sin( 5 * 2 pi ft + phi_5) + P_6 sin( 6 * 2 pi ft + phi_6) + ...
This certainly builds a function which is periodic with period T, since each sine wave repeats every T. That any curve can be built in this way is illustrated by this picture:
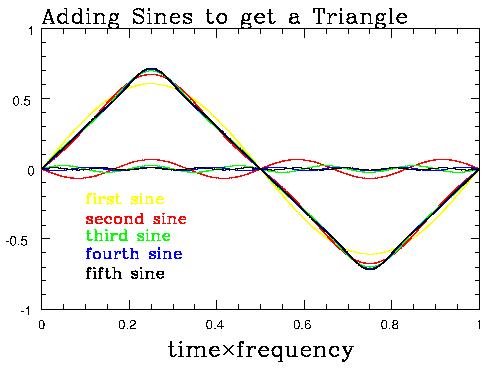
which shows how adding several sine waves with the right coefficients gets you to a triangle wave. It takes an infinite number to do it exactly but you can see that a not-so-big number does a surprisingly good job.
The individual sine waves which build up the complex tone are called the harmonics of the tone. Everyone agrees that the sine wave with the same frequency as the tone is called the fundamental of the tone. There are two nomenclatures for the higher multiples. Either they are called:
You will also hear people referring to the fundamental and the overtones (with the same confusiong about nomenclature). For a periodic sound, "overtone" and "harmonic" are synonymous. The difference is that some non-periodic sounds (many percussion sounds, for instance) are composed as the sum of sine waves, but with the frequencies of the higher components not integer (counting number) multiples of the fundamental. In such case we call the other things overtones, and reserve the word "harmonic" for the case where they are integer (counting number, 1,2,3,4,5...) multiples of the fundamental. A more nontrivial example is shown next: building the sounds "ooo" (upper 3) and "eee" (lower 3) out of Fourier components:
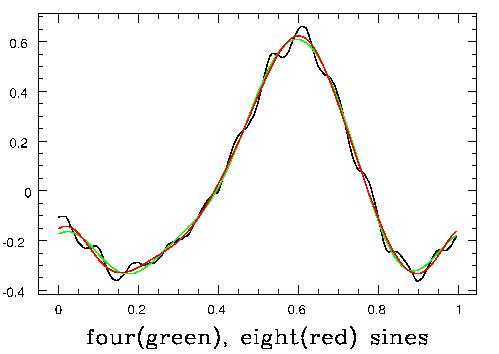
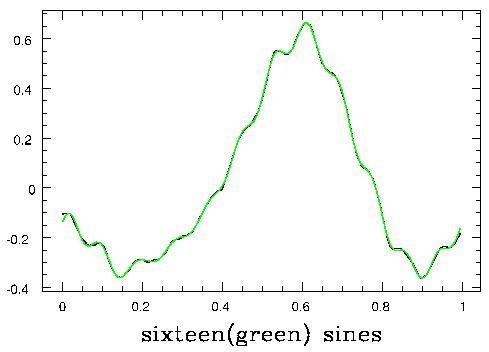
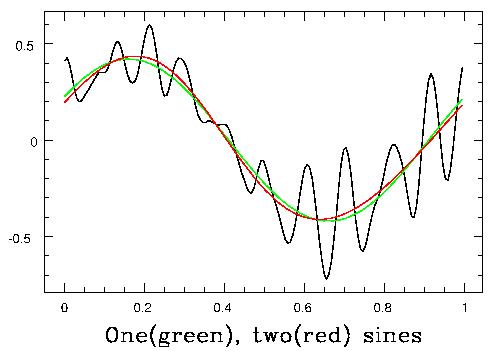
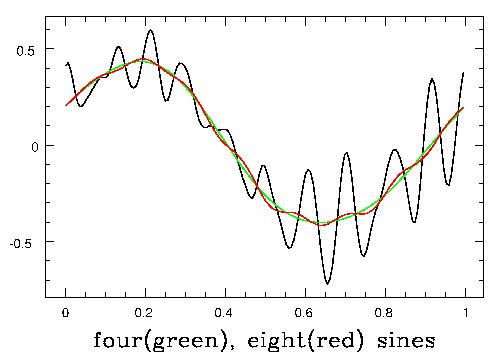
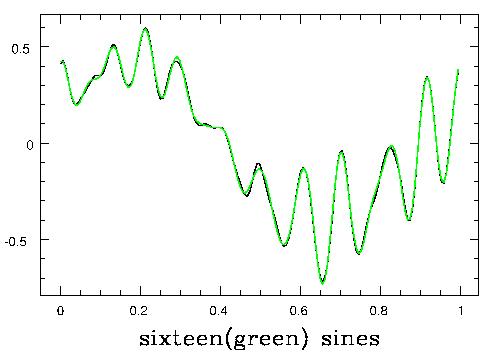
I should also show what it sounds like as you add one after another Fourier component to produce a complex wave. This is done for a sawtooth wave, which has a lot of overtone structure, in this MP3 file, which plays 1, 2, 3, 5, and 10 of the overtones before playing the whole sawtooth.
What happens when a complex tone arrives at your ear? The answer is that you can use linearity to think about what each harmonic does, separately. The behavior of the cochlea is almost linear. We will see later that it is not perfectly linear, but don't worry about that now. Therefore, for a complex tone, the excitation of the cochlea will be the excitations of the points corresponding to each harmonic, with sizes corresponding to how loud each harmonic is. To illustrate:
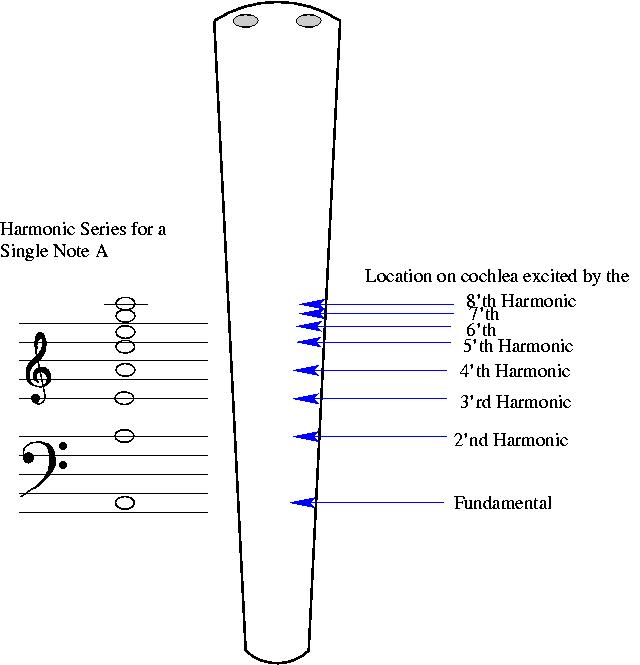
Your ear automatically recognizes this tower of spots of excitations as arising from a single complex tone. Your brain extracts the fundamental and gives this to you as "the" frequency, and you sense or feel the extra information about the relative loudnesses of the harmonics as the sound's timbre.
Note that the harmonics get closer and closer together in terms of their pitch. This is because what is important to perception is the log of the ratio of frequency. The ratio of the 2'nd to 1'st harmonic is 2/1=2; of 3'rd to 2'nd is 3/2=1.5; of 4'th to 3'rd is 4/3=1.33, and so on. [Musically, the separations are: 2/1=octave, 3/2=perfect fifth, 4/3=perfect fourth, 5/4=major 3'rd, 6/5=minor 3/rd, but the thirds are not tempered by more than the JND, as we will discuss in future.]