Übersicht
Structure of exotic nuclei
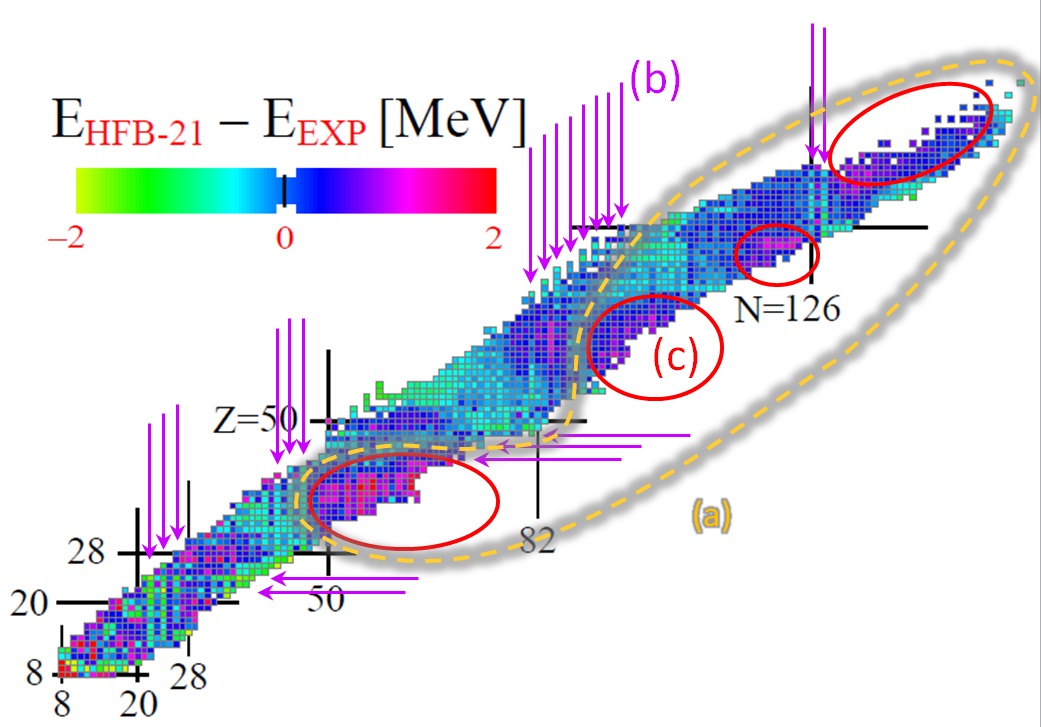 Although it is well-established
that almost half of the heavy elements are produced by the rapid
neutron-capture process (r-process), the quest to identify the actual
astrophysical site still ongoing [
1]. R-process models require nuclear physics input for a large number of
nuclei that have extreme neutron excess and stretch up to the limits of the
nuclear chart. Such nuclei lie far beyond capabilities of experimental
facilities in any foreseeable future, and hence r-process
simulations rely on theoretical predictions of
various nuclear properties. Nuclear masses are particularly important as they
determine thresholds of all nuclear reactions. These include neutron capture,
beta-decay and fission. They determine r-process path and the
final shape of the r-process abundances [2].
Although it is well-established
that almost half of the heavy elements are produced by the rapid
neutron-capture process (r-process), the quest to identify the actual
astrophysical site still ongoing [
1]. R-process models require nuclear physics input for a large number of
nuclei that have extreme neutron excess and stretch up to the limits of the
nuclear chart. Such nuclei lie far beyond capabilities of experimental
facilities in any foreseeable future, and hence r-process
simulations rely on theoretical predictions of
various nuclear properties. Nuclear masses are particularly important as they
determine thresholds of all nuclear reactions. These include neutron capture,
beta-decay and fission. They determine r-process path and the
final shape of the r-process abundances [2].
One of the most successful global nuclear physics approaches is the self-consistent mean-field (SCMF) model based on Hartree-Fock-Bogolyubov (HFB) variational approach with energy density functionals (EDF). The objective of the SCMF approach is to transform the intricate problem of strongly interacting system of protons and neutrons into a much less complex picture of non-interacting particles moving in a self-consistent single-particle potential. Such a model is expected to be reliable in extrapolations to unknown nuclei.
In our group we study the properties of exotic nuclei using the EDF theory as a nuclear structure model, and nowadays we are focused in the following topics:
The final aim of these studies is to provide a more robust description of the major nuclear properties entering as an input in heavy nuclei nucleosynthesis calculations. In order to reach such a goal, our group is constantly involved in improving the understanding of the properties of exotic nuclei.
Structure of exotic nuclei
 Although it is well-established
that almost half of the heavy elements are produced by the rapid
neutron-capture process (r-process), the quest to identify the actual
astrophysical site still ongoing [
1]. R-process models require nuclear physics input for a large number of
nuclei that have extreme neutron excess and stretch up to the limits of the
nuclear chart. Such nuclei lie far beyond capabilities of experimental
facilities in any foreseeable future, and hence r-process
simulations rely on theoretical predictions of
various nuclear properties. Nuclear masses are particularly important as they
determine thresholds of all nuclear reactions. These include neutron capture,
beta-decay and fission. They determine r-process path and the
final shape of the r-process abundances [2].
Although it is well-established
that almost half of the heavy elements are produced by the rapid
neutron-capture process (r-process), the quest to identify the actual
astrophysical site still ongoing [
1]. R-process models require nuclear physics input for a large number of
nuclei that have extreme neutron excess and stretch up to the limits of the
nuclear chart. Such nuclei lie far beyond capabilities of experimental
facilities in any foreseeable future, and hence r-process
simulations rely on theoretical predictions of
various nuclear properties. Nuclear masses are particularly important as they
determine thresholds of all nuclear reactions. These include neutron capture,
beta-decay and fission. They determine r-process path and the
final shape of the r-process abundances [2].
One of the most successful global nuclear physics approaches is the self-consistent mean-field (SCMF) model based on Hartree-Fock-Bogolyubov (HFB) variational approach with energy density functionals (EDF). The objective of the SCMF approach is to transform the intricate problem of strongly interacting system of protons and neutrons into a much less complex picture of non-interacting particles moving in a self-consistent single-particle potential. Such a model is expected to be reliable in extrapolations to unknown nuclei.
In our group we study the properties of exotic nuclei using the EDF theory as a nuclear structure model, and nowadays we are focused in the following topics:

- Enhance the accuracy in theoretical calculations of nuclear masses across the whole isotopic chart by tackling and resolving some of the remaining main issues with the currently employed SCMF models. These include the treatment of odd and odd-odd nuclei at the same self-consistent level as even-even nuclei [5] and the inclusion of beyond mean field effects [6].
- Improve the theoretical description of the fission process within the EDF theory. In the fission decay the parental nucleus splits in two or more fragments of similar mass. This process is driven by a delicate balance between the repulsive Coulomb force of protons and the strong force binding nucleons together. Moreover, quantum mechanical effects such as shell effects and levels densities strongly influence the fission properties of the nucleus. Our goal is to provide a reliable description of this phenomena using the EDF theory [7, 8] and to provide a systematic data set of the fission properties (e.g. fission barriers, fragments distributions, rates, ...) that are relevant in astrophysical calculations.
- Provide global calculations of beta-decay rates for r-process nuclei that consistenly consider both Gamow-Teller and forbidden transitions [9]
The final aim of these studies is to provide a more robust description of the major nuclear properties entering as an input in heavy nuclei nucleosynthesis calculations. In order to reach such a goal, our group is constantly involved in improving the understanding of the properties of exotic nuclei.
- [1] Thielemann F-K, et al., Prog. Part. Nucl. Phys. 66, 346 (2011).
- [2] Goriely S and Martinez-Pinedo G, Nucl. Phys. A1, 1 (2015).
- [3] Bender M, Heenen P-H, Reinhard P-G, Rev. Mod. Phys. 75, 121 (2003).
- [4] Arzhanov A, Rodriguez TR, Martinez-Pinedo G, in preparation (2016).
- [5] Robledo LM, Bernard R, and Bertsch GF, Phys. Rev. C86, 064313 (2012).
- [6] Rodriguez TR, Arzhanov A, Martinez-Pinedo G, Phys. Rev. C91, 044315 (2015).
- [7] Giuliani SA, Robledo LM and Rodríguez-Guzmán R., Phys. Rev. C90, 054311 (2014).
- [8] Giuliani SA and Robledo LM, Phys. Rev. C88, 54325 (2013).
- [9] T. Marketin, L. Huther, and G. Martínez-Pinedo, Phys. Rev. C93, 025805 (2016).


