Weak interactions in astrophysics

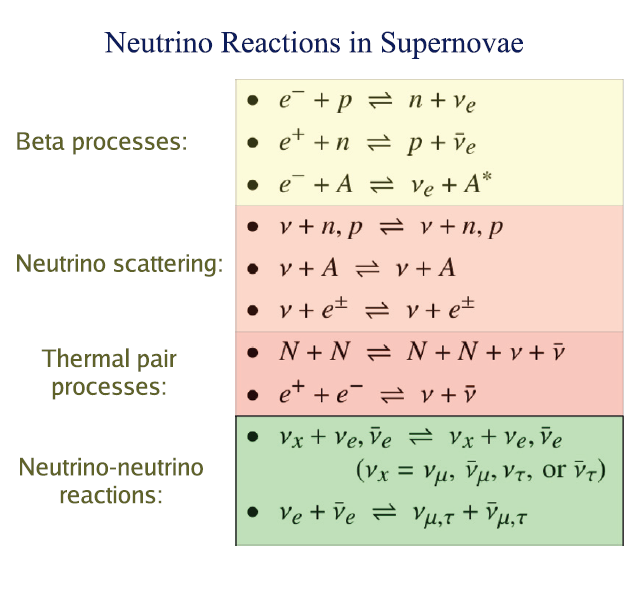The weak interaction is a mechanism acting on quarks and leptons. The massive exchange particles by which the interaction can be mediated is either the neutral Z⁰ or the charged W^+/- bosons, where the former results into scattering reactions where simply momentum and energy is exchanged, and the latter into absorption reactions in which the particle species in the outgoing channel will differ from the incoming ones (c.f. e.g. [1]) . On a much less fundamental level, weak interactions are also evident for composite particles made of quarks, i.e. the hadrons. Particular famous reactions in nuclear physics stemming from an underlying weak interaction process are for instance beta decay of neutrons (n → p + e^- + ν_e) or electron capture on protons (p + e^- → n + ν_e) .

In particular both of these weak reactions not only play a role in nuclear physics, but on a much larger scale also affect the dynamics of core-collapse supernovae in astrophysics. In the late phase of the life of a heavy star (M > 8 M_☉), the internal pressure from the degenerate electron gas will eventually become incapable of compensating the gravitational pressure, resulting into the collapse of the star. As the density increases in the core due to the compression, electron capture reactions on nuclei become increasingly likely and lead to an increasing production of electron neutrinos, which initially can escape and thus further accelerate the collapse. Eventually the core will be compressed to a state of density at which the nuclei break up and neutrons and protons form a dense state matter. At these high densities, neutrinos created inside the center of the star become trapped, incapable of escaping.

Understanding the importance of different possible weak interaction processes thus is also important to understand the dynamics of the postbounce phase of core-collapse supernovae , the underlying nucleosynthesis, and the neutrino signal on Earth. The neutrino gas in supernova simulations is described by the so called Boltzmann transport equation with values for opacities (i.e. inverse mean free paths) of the neutrinos stemming from the particular reactions of interest. The opacities can be calculated from an integral over the product of statistical weighting functions and the square of a transition matrix element stemming directly from a field theoretical inspection of the interaction (c.f. [3,4]). Improvements of the understanding of the role of weak reactions in core-collapse supernovae thus can be made on various levels.
For instance, although there is currently an established set of reactions considered important for supernova events (c.f. [2]), further reactions might still play important roles [5]. It was only until recently that the channel of the inverse neutron decay was found to have a significant opacity contribution in the low-energy regime at neutrino trapped settings.
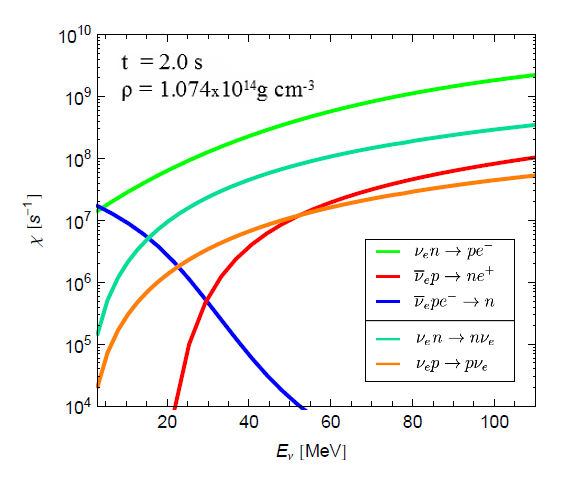First CCSN simulations including this new channel hint towards an increase of the average energy in the spectrum of radiated electron antineutrinos in comparison to simulations without. Further, many opacities are often calculated based upon various approximations or in some cases by using heuristic expressions. Improving the calculational procedures and underlying expressions for the opacities thus might still further yield valuable new results. Going even further, on the most fundamental level weak interaction processes are governed by respective transition matrix elements which can be obtained from field theoretical calculations. The matrix elements are often further simplified by assuming certain approximations and in some cases depend on the particular underlying models of interactions in use. Thus it might be of further interest to find out whether or not the the treatment of the interaction self can be further refined. At the end of the day we hope that we are able to include weak reactions to such a degree of consistency in CCSN simulations, that we will be able to realistically simulate the essential dynamics and deduce realistic values for observables.